1 Dimensional Bin Sorting Class

This class can perform a one dimensional bin packing. It could be used to: Sort pakages of a certain weight into containers that can carry a given weight, cut 2x4s of a certain length into the required pieces, fill floppy disks with a list of files... A mix between standard Best Fit and Worst Fit algorithms is used. Data must be entered and sorted descending before calling the main PackBins Sub.

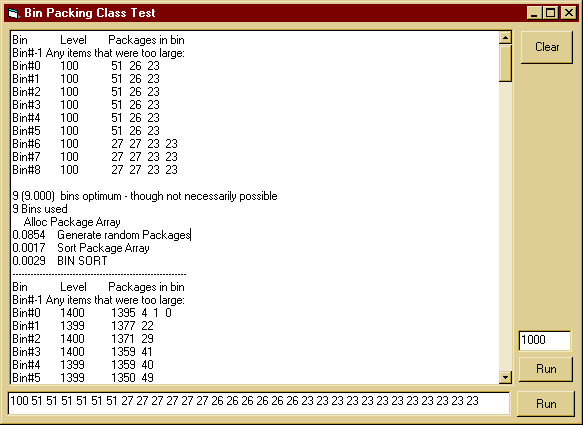
Time Complexity (TC) of this function where N = # of items B = # of bins needed = 1 + int(sum(1 to N) of itemsize / BinCapacity) TC = N * B (i.e. we loop through the N items comparing most of them to each bin) On my computer: 1000items-> ~200bins ==> 200,000 .06sec 5000items->~1000bins ==> 5,000,000 1.50sec If the average size of an item is 1/2 bin size then TC = N * N/2 or more generally: TC = N * N * Save% (where S is the percentage of average item size relative to bin capacity) TC = N 2 * Save% So if average item size doesn't change doubling the number of items quadruples time spent. Using the second test time above would mean 5 million items would take 17.4 days to sort (5mil/5000 —> 10002 * 1.5sec). However, we could assume that not much is gained by considering all items together. You could instead break it down to 5000 reps of the 1000 item problem which would give 0.06s * 5000 = 5min. You might save the results of each repetition, but remove the items in the last bin if not near full and return them to the items remaining to be sorted. Also note that as S is decreased the number of bins needed will approach the optimum. And as S is increased the assumption above is less true; it becomes more important to check as many items as possible to reduce the number of bins needed. I lack the math skills to prove it, but it's not difficult to see that if you have 1000 items with values ranging from 0 to 1000 and the bin capacity is 1000, there will be many bins with a large first item that won't have a near perfect match which will result in extra bins needed. So given a maximum item size Smax there should be a point at which checking more items causes a huge time penalty without doing much to optimize the number of bins needed: Iopt = Smax * M (where if Save% is large M > 1). One last note: It is perfectly possible that the number of bins needed far excedes the predicted optimum without implying that the sort did a bad job. Consider a problem where bin capacity is 10 and you have 4 items of size 6. 28/10 predicts that 3 bins will be needed while it is clear that 4 bins are needed.

Download source code with a test app (11KB)

Main function of class module

Public Function PackBins()
    Dim i As Long, j As Long, tot As Long
    Dim iBestBin As Long, iWorstBin As Long, qBestBin As Long, qWorstBin As Long, x As Long
    Dim iSize As Long '=m_Items(i).Size
    Dim prevUbound As Long
    
    pTightenPackageList
    If UBound(m_Items) = 0 Then '1 item
        ReDim m_Bins(m_iUItem To m_iUItem) 'so BinsNeeded will give correct val
        Exit Function
    End If
    
    If m_BinReasonablyFull = 0 Then m_BinReasonablyFull = 0.95 * m_BinCapacity
    For i = 0 To UBound(m_Items)
        If m_Items(i).size <= m_BinCapacity Then tot = tot + m_Items(i).size
    Next
    'start with one less than min bins necessary to hold all items
    'when remainder of tot / m_BinCapacity < 0.5
    ReDim m_Bins(Int(tot / m_BinCapacity) + CLng((tot Mod m_BinCapacity) < m_BinCapacity / 2))
    
    Debug.Print FormatNumber(tot / m_BinCapacity, 3) & "(i.e. " & Int(tot / m_BinCapacity) + IIf(tot Mod m_BinCapacity, 1, 0) & ")  bins optimum - though not necessarily possible"
    
    
    'place all items over 1/2 capacity in their own bin
    qBestBin = Int(m_BinCapacity / 2)
    For i = 0 To UBound(m_Items)
        iSize = m_Items(i).size
        If iSize > qBestBin Then
            If iSize <= m_BinCapacity Then
                m_Items(i).lBin = i
                If i > UBound(m_Bins) Then pNewBin
                m_Bins(i) = iSize 'mark bin usage
            Else
                m_Items(i).lBin = -1 'oversized
            End If
        Else
            Exit For ' <= 1/2 bin capacity
        End If
    Next
    
    'place the rest of the items
    For i = i To UBound(m_Items)
        'loop until a bin has been found
        m_Items(i).lBin = -1 'no bin chosen yet
        
            iBestBin = -1 'best bin index and flag that best bin found
            iWorstBin = -1 'worst bin index and flag that fits in bin
            qBestBin = m_BinReasonablyFull - 1 'a best bin has to be > this
            qWorstBin = m_BinCapacity + 1
            iSize = m_Items(i).size
            j = 0 'current bin to check
            Do
                
                x = m_Bins(j) + iSize
                'if fits in bin
                If x <= m_BinCapacity Then

                    'is it most full bin
                    If x > qBestBin Then 'NOW qBestBin always= m_BinReasonablyFull-1
                        m_Items(i).lBin = j
                        m_Bins(j) = x ' m_Bins(j) + iSize
                        Exit Do
                    End If

                    'is it least full bin
                    If x < qWorstBin Then
                        qWorstBin = x
                        iWorstBin = j
                    End If

                End If
    
                'if current bin is empty or last bin and don't need new one it's time to decide where to place item
                If (m_Bins(j) = 0) Or (j = UBound(m_Bins)) Then
                    If iWorstBin >= 0 Then
                        m_Items(i).lBin = iWorstBin
                        m_Bins(iWorstBin) = m_Bins(iWorstBin) + iSize
                        Exit Do
                    Else 'didn't fit - place in the empty bin or in new bin
                        If m_Bins(j) <> 0 Then
                            'we need a new bin (rare since we start with min bins
                            pNewBin
                            j = j + 1
                        End If
                        m_Items(i).lBin = j
                        m_Bins(j) = m_Bins(j) + iSize
                        Exit Do
                    End If
                    
                End If
                
                'try next bin
                j = j + 1
            Loop 'While m_Items(i).lBin = -1 'now exit do takes care 15%faster in IDE
    Next
    
    '--------------------------------------------------------------
    If m_Bins(UBound(m_Bins)) = 0 And UBound(m_Bins) > 0 Then
        ReDim Preserve m_Bins(UBound(m_Bins) - 1)
    End If
    'try and place last items as 1st fit
    'keep last bin as empty as possible
    x = 0 ': j = 0
    i = 0
    Do 'For i = 0 To UBound(m_Items)
        If m_Items(i).lBin = UBound(m_Bins) Then
            If x Then
                iSize = m_Items(i).size
                For j = 0 To UBound(m_Bins) - 1
                    If m_Bins(j) + iSize <= m_BinCapacity Then
                        m_Bins(j) = m_Bins(j) + iSize
                        m_Bins(UBound(m_Bins)) = m_Bins(UBound(m_Bins)) - iSize
                        m_Items(i).lBin = j
                        Debug.Print "moved an item out of last bin"
                        'leave if only the first item remains in last bin
                        If m_Bins(UBound(m_Bins)) = x Then Exit Do
                        Exit For
                    End If
                Next
            Else
                x = m_Items(i).size  'flag that we found and skipped first (largest) item in last bin
            End If
        End If
        i = i + 1
    Loop While i <= UBound(m_Items) 'Next
'    SortPackagesByBin 'let user call this so we can see how binsort was executed
Debug.Print
End Function